Crowbar - an open-source editor
- Thread starter NoodleCollie
- Start date
The variables passed into the shaders. I think that's what they're called.
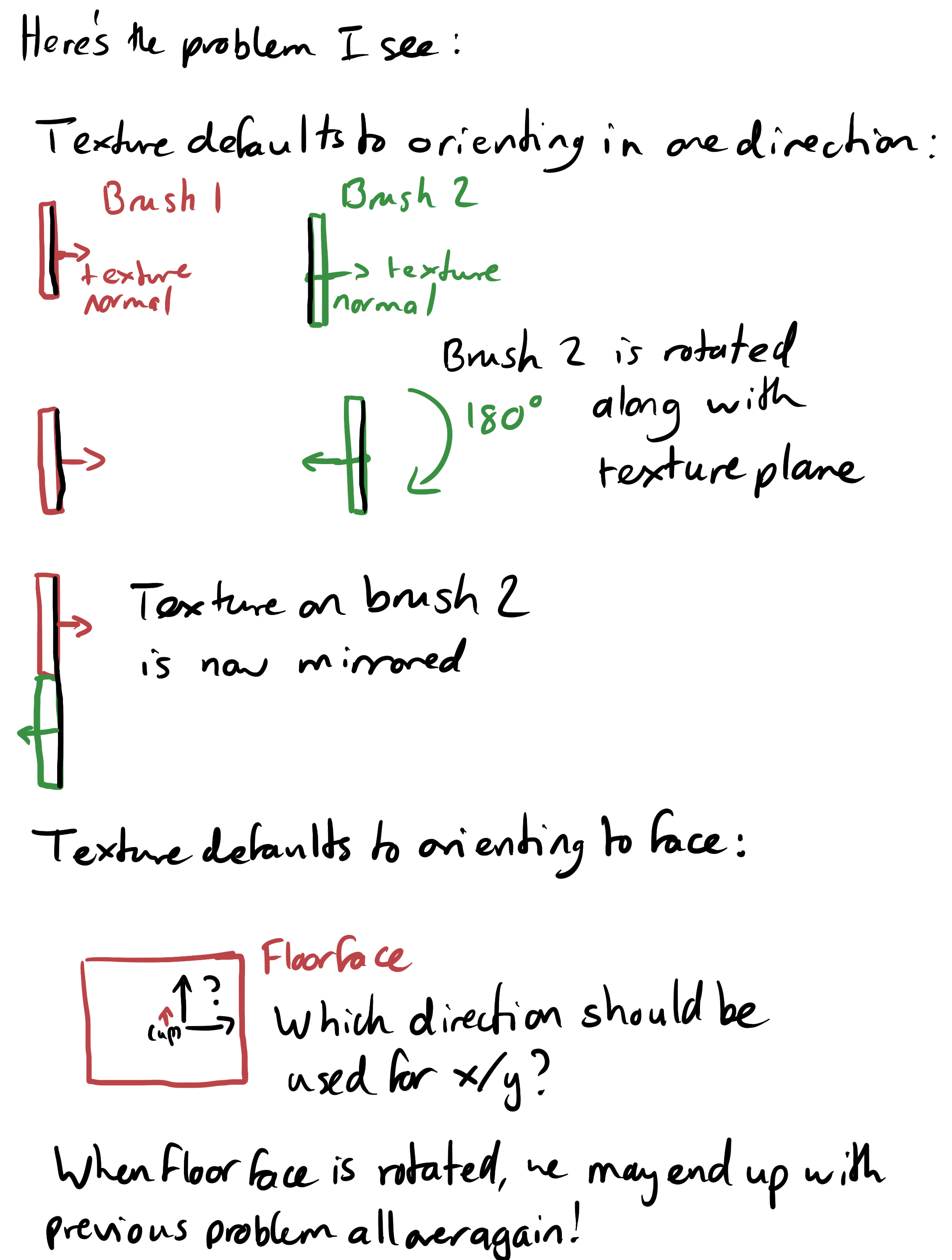
I've looked into how Hammer deals with textures and the VMF specifies the U and V axes with 3D vectors. This means that the texture plane can exist in any 3D plane and the appearance on a brush face is a result of a projection from the texture plane onto the face plane. I'm trying to get my head around what this means for brush and face transformations - when a brush face is rotated, should the texture plane rotate with it by default? What should the default orientation of the texture plane be? I'm not sure I fully understand the questions I have, but here's a diagram of some of the things that are bugging me:
stegarootbeer
L2: Junior Member
- Jan 15, 2012
- 78
- 100
On the subject of textures, any chance you can make painting alpha look more like it does in game instead of just a fade like it is in hammer?
The L4D2 editor manages to do that, so it's probably something we can do.
Here are my thoughts on the overall architecture + how data is moved around:
Last edited:
I like to be able to draw diagrams and stuff, but yeah I'll use proper text next time. SAI doesn't support them so I didn't bother loading into another graphics package this time.
EDIT: Updated.
EDIT: Updated.
Last edited:
Hammer has options for world aligned vs face aligned, the default is world align, so the texture appears as you might expect when looking down three of the axes, and when looking up at them you're getting a flipped image.
It then has options for texture lock, and texture scale lock. With these off, any time a brush is manipulated, the texture is reprojected from whatever it was before so rotating a brush face more than 45 degrees will change which axis the texture is projected from since it picks the one it's closest to by default.
I almost always have texture lock off but if you keep it on, the texture on a face that is rotated after creation rotates with it, so if you rotate it 180 you'll get it rotated rather than flipped like you described above.
Welp, someone beat me to a custom map editor. http://gamebanana.com/threads/19290...buffer&utm_medium=twitter&utm_campaign=Buffer
Looks pretty cool but crashes right now as it can't find the HL textures. Gotta test it out properly later.
Looks pretty cool but crashes right now as it can't find the HL textures. Gotta test it out properly later.
Last edited:
For anyone fancying an interesting (but in some cases heavy-going) Mathsy read, I've found a potentially very useful library: http://doc.cgal.org/latest/Manual/packages.html
I did actually consider it, but Sledge is written in C# which was exactly the language I was using before I switched over to Qt and C++ way back at the start of this thread in order to get cross-platform compatibility, so switching back would seem kind of redundant. Also I've grown to quite like Qt. 
For anyone interested in shaders, I mocked up the Hammer 2D viewport in GLSL as an exercise in learning the language. Click and drag to move the grid. Changing the zoom value and recompiling the code will change the zoom level of the grid. (In an actual program the zoom value would be an input to the shader, but I'm not sure whether you can provide inputs to this sandbox site). The code should hopefully be commented enough to follow easily.
https://www.shadertoy.com/view/ld23Dm
If you don't know what GLSL (OpenGL Shading Language) is, basically it allows you to write a small program which runs on the graphics card (a shader) which will perform the calculations to determine the colour of each pixel when it's rendered (the fragment shader) or the position of each vertex in screen space (the vertex shader).
https://www.shadertoy.com/view/ld23Dm
If you don't know what GLSL (OpenGL Shading Language) is, basically it allows you to write a small program which runs on the graphics card (a shader) which will perform the calculations to determine the colour of each pixel when it's rendered (the fragment shader) or the position of each vertex in screen space (the vertex shader).
Last edited:
Thought I might share some recent thoughts I've had on structuring the 3D world, as it seems to help my thought process:
To make tasks such as determining visibility and getting objects by their 3D location easier, data structures called octrees are often used. These are basically made out of cubes, representing 3D space, which are recursively subdivided: the largest, parent cube is split into eight equally-sized child cubes which completely fill its volume, and each of these is split into eight children, and so on until a desired level of granularity is reached. This structure corresponds conceptually (and in code implementation) to a tree, where each node corresponds to a 3D cube, and where each non-leaf node will have eight children (hence "oct" tree). They're pretty cool and you should Google them.
There are two very useful things about an octree. The first is that, given an x, y and z value, you can address any leaf node in the octree very efficiently, in contrast to a simple list where a full, linear search would be required each time in order to match the x, y and z values. The second useful thing is that, if a parent node in the octree doesn't matter to your calculations, then the children will not either. This is easily demonstrated when considering which nodes might be visible to a perspective camera: if a larger cube is completely outside your field of vision, it's clear that all its children (contained entirely inside it) will not be visible either. The consequences of this are that, if you determine early on in your calculations that a given octree node is not visible, there is absolutely no need for you to check whether any of its children are visible because you know instantly that they are not. You can discard those branches of the tree entirely, saving yourself potentially large amounts of processing time.
So, given an octree, how should arbitrary objects be stored in it? Each 3D object can be thought of as having an axially aligned bounding box, which corresponds to the cuboid volume between the two 3D components with the largest and smallest co-ordinate values respectively. The bounding box is the coloured box that you see when you move far enough away from a prop in Hammer, and it guarantees that all the 3D components of the object are contained within the box. To store an object in an octree, we can record a reference to the object in each leaf node (smallest cube) that is either intersected or fully enclosed by the object's bounding box. This does duplicate information into multiple leaf nodes if the object is too large or in the wrong place to be contained within a single node, but the alternative is to have irregularly-sized nodes which sounds very complicated to me, and would not be particularly well-suited to a dynamic 3D scene such as a level editor.
However, just having an octree on its own isn't enough to store objects; we also need to know how large the octree should be. A simple way of specifying this is to decide on the distance between the origin of the octree (the centre of the root node, or largest parent cube) and its outer edge, in each axis (which I'll call the magnitude). Hammer's co-ordinates range from -16,384 to 16,384 in each dimension, so an octree that would cover all of this would have magnitude 16,384. The final piece of information is how many leaf nodes should be present in each axis; for leaf nodes of size 128x128x128 units each in a Hammer-sized octree, the tree would need 256x256x256 individual leaf nodes.
Given all of this information, it is possible to remap a given 3D co-ordinate to index an octree node with an integer x, y and z value. Octree nodes can be though of as utilising a 3D array, with elements (leaf nodes, in this case) specified by a value in each of the three axes. With the code below as an example (which I won't go into in great depth), 3D co-ordinates can be easily translated to a 3-part octree node index.
All you really need to worry about is that, with this code, we can translate the maximum and minimum 3D co-ordinates of an object's bounding box (for example, (100, 310, 304)<->(150, 443, 512)) into maximum and minimum octree node indices (for example, [1,3,3]<->[1,4,5]). Any nodes between these indices should record the object as being present within them, as the nodes are within or are intersecting the object's bounding box (in this example: [1,3,3], [1,3,4], [1,3,5], [1,4,3], [1,4,4] and [1,4,5]). If both the maximum and minimum bounding box co-ordinates translate to exactly the same octree node index, we know that the object is completely contained within that leaf node!
As mentioned before, an octree makes it easy to "index by location" - if a 3D location is known, we can translate it to a leaf node index and get the list of objects present in that node very efficiently. It does not, however, allow for efficiency the other way around: if we are given an object and asked to find which nodes it is present in, we may need to look through each and every leaf node to see if the object is recorded within. To solve this problem we could ask for the object's bounding box too, which would allow us to calculate the range of leaf nodes as per the code above, but a problem arises if the object (which is external to the octree itself) has been changed: if the octree hasn't been updated, the object's new bounding box will be in a different position to that recorded in the octree. Using this new bounding box, the nodes returned by the octree as being occupied by this bounding box may be different from the actual nodes the object is recorded in. We are relying on the user of the octree to always maintain and pass in correct data. Not good!
To remedy this, we can store the bounding box of every object we put into the octree in a hash table, with the key of the table element being the object stored. A hash table is simply a list indexed by unique keys, and with each key holding a corresponding value, which allows quick access to arbitrary objects in a similar way to an array; whereas arrays are indexed by integer, from 0 to length-1, hash tables use a key (formed by generating a hash code for an arbitrary object or number) to address an element and return the associated value for this key in constant time (read: very quickly). The crucial difference the hash table provides is that we don't need to rely on the bounding box of the passed object being correct for the current state of the octree: if we keep the hash table updated with the correct bounding boxes every time an object is added, removed or changed, the bounding box stored in the hash table will always be correct with respect to the nodes in which its object is recorded.
For instance, if we add an object with bounding box (1,1,1)<->(3,3,3), the object and bounding box will be added to a new hash table element, using the hash of the object as the key and and bounding box as the value. Later on, if we submit a changed bounding box to the octree for that object (implying that we've translated the object), we can look up the object in the hash table to find its previously valid bounding box, remove the object from all leaf nodes in which it was previously recorded, then re-record the object reference in all the new nodes corresponding to our new bounding box. We don't need to ask the user of the octree to pass in a bounding box for the object, and we don't need to worry about all the potential problems which may occurr if the bounding box they passed in wasn't correct.
To make tasks such as determining visibility and getting objects by their 3D location easier, data structures called octrees are often used. These are basically made out of cubes, representing 3D space, which are recursively subdivided: the largest, parent cube is split into eight equally-sized child cubes which completely fill its volume, and each of these is split into eight children, and so on until a desired level of granularity is reached. This structure corresponds conceptually (and in code implementation) to a tree, where each node corresponds to a 3D cube, and where each non-leaf node will have eight children (hence "oct" tree). They're pretty cool and you should Google them.
There are two very useful things about an octree. The first is that, given an x, y and z value, you can address any leaf node in the octree very efficiently, in contrast to a simple list where a full, linear search would be required each time in order to match the x, y and z values. The second useful thing is that, if a parent node in the octree doesn't matter to your calculations, then the children will not either. This is easily demonstrated when considering which nodes might be visible to a perspective camera: if a larger cube is completely outside your field of vision, it's clear that all its children (contained entirely inside it) will not be visible either. The consequences of this are that, if you determine early on in your calculations that a given octree node is not visible, there is absolutely no need for you to check whether any of its children are visible because you know instantly that they are not. You can discard those branches of the tree entirely, saving yourself potentially large amounts of processing time.
So, given an octree, how should arbitrary objects be stored in it? Each 3D object can be thought of as having an axially aligned bounding box, which corresponds to the cuboid volume between the two 3D components with the largest and smallest co-ordinate values respectively. The bounding box is the coloured box that you see when you move far enough away from a prop in Hammer, and it guarantees that all the 3D components of the object are contained within the box. To store an object in an octree, we can record a reference to the object in each leaf node (smallest cube) that is either intersected or fully enclosed by the object's bounding box. This does duplicate information into multiple leaf nodes if the object is too large or in the wrong place to be contained within a single node, but the alternative is to have irregularly-sized nodes which sounds very complicated to me, and would not be particularly well-suited to a dynamic 3D scene such as a level editor.
However, just having an octree on its own isn't enough to store objects; we also need to know how large the octree should be. A simple way of specifying this is to decide on the distance between the origin of the octree (the centre of the root node, or largest parent cube) and its outer edge, in each axis (which I'll call the magnitude). Hammer's co-ordinates range from -16,384 to 16,384 in each dimension, so an octree that would cover all of this would have magnitude 16,384. The final piece of information is how many leaf nodes should be present in each axis; for leaf nodes of size 128x128x128 units each in a Hammer-sized octree, the tree would need 256x256x256 individual leaf nodes.
Given all of this information, it is possible to remap a given 3D co-ordinate to index an octree node with an integer x, y and z value. Octree nodes can be though of as utilising a 3D array, with elements (leaf nodes, in this case) specified by a value in each of the three axes. With the code below as an example (which I won't go into in great depth), 3D co-ordinates can be easily translated to a 3-part octree node index.
Code:
template< typename T, int AS >
const T& Octree<T,AS>::atPosition(int magnitude, const QVector3D &worldPos) const
{
// Remap x, y and z to octree indices.
int x = mapToNodeIndex(magnitude, worldPos.x());
int y = mapToNodeIndex(magnitude, worldPos.y());
int z = mapToNodeIndex(magnitude, worldPos.z());
// Return the list of objects from the node at this index.
return at(x, y, z);
}
template< typename T, int AS >
int Octree<T,AS>::mapToNodeIndex(int magnitude, float inValue) const
{
// Translate magnitude and inValue into co-ordinates that are easier to work with.
int extent = 2 * magnitude;
float newIn = (float)magnitude + inValue;
// Get the index.
return mapToNodeIndex(extent, size(), newIn);
}
template< typename T, int AS >
static int Octree<T,AS>::mapToNodeIndex(int extent, int nodeCount, float inValue)
{
// inValue / extent gives the fraction along the extent from -magnitude to +magnitude that the inValue lies.
// Multiplying this by nodeCount and flooring will give us the node index along this extent.
int ret = qFloor((inValue*nodeCount)/extent);
// Clamp the return value.
if ( ret < 0 ) ret = 0;
else if ( ret >= nodeCount ) ret = nodeCount - 1;
// Return it.
return ret;
}All you really need to worry about is that, with this code, we can translate the maximum and minimum 3D co-ordinates of an object's bounding box (for example, (100, 310, 304)<->(150, 443, 512)) into maximum and minimum octree node indices (for example, [1,3,3]<->[1,4,5]). Any nodes between these indices should record the object as being present within them, as the nodes are within or are intersecting the object's bounding box (in this example: [1,3,3], [1,3,4], [1,3,5], [1,4,3], [1,4,4] and [1,4,5]). If both the maximum and minimum bounding box co-ordinates translate to exactly the same octree node index, we know that the object is completely contained within that leaf node!
As mentioned before, an octree makes it easy to "index by location" - if a 3D location is known, we can translate it to a leaf node index and get the list of objects present in that node very efficiently. It does not, however, allow for efficiency the other way around: if we are given an object and asked to find which nodes it is present in, we may need to look through each and every leaf node to see if the object is recorded within. To solve this problem we could ask for the object's bounding box too, which would allow us to calculate the range of leaf nodes as per the code above, but a problem arises if the object (which is external to the octree itself) has been changed: if the octree hasn't been updated, the object's new bounding box will be in a different position to that recorded in the octree. Using this new bounding box, the nodes returned by the octree as being occupied by this bounding box may be different from the actual nodes the object is recorded in. We are relying on the user of the octree to always maintain and pass in correct data. Not good!
To remedy this, we can store the bounding box of every object we put into the octree in a hash table, with the key of the table element being the object stored. A hash table is simply a list indexed by unique keys, and with each key holding a corresponding value, which allows quick access to arbitrary objects in a similar way to an array; whereas arrays are indexed by integer, from 0 to length-1, hash tables use a key (formed by generating a hash code for an arbitrary object or number) to address an element and return the associated value for this key in constant time (read: very quickly). The crucial difference the hash table provides is that we don't need to rely on the bounding box of the passed object being correct for the current state of the octree: if we keep the hash table updated with the correct bounding boxes every time an object is added, removed or changed, the bounding box stored in the hash table will always be correct with respect to the nodes in which its object is recorded.
For instance, if we add an object with bounding box (1,1,1)<->(3,3,3), the object and bounding box will be added to a new hash table element, using the hash of the object as the key and and bounding box as the value. Later on, if we submit a changed bounding box to the octree for that object (implying that we've translated the object), we can look up the object in the hash table to find its previously valid bounding box, remove the object from all leaf nodes in which it was previously recorded, then re-record the object reference in all the new nodes corresponding to our new bounding box. We don't need to ask the user of the octree to pass in a bounding box for the object, and we don't need to worry about all the potential problems which may occurr if the bounding box they passed in wasn't correct.
henke37
aa
- Sep 23, 2011
- 2,075
- 515
The problem with octrees is that they don't do occlusion filtering. And given how much level geometry can be inside the viewing frustum but occluded by closer geometry...
Also, there is no rule saying that the size of each octree level has to be fixed. You can dynamically divide as desired. This allows you to merge leaf nodes when only one of them has something in it.
Also, there is no rule saying that the size of each octree level has to be fixed. You can dynamically divide as desired. This allows you to merge leaf nodes when only one of them has something in it.