- Aug 7, 2017
- 58
- 2
This is a bit of a ramble, I'm sorry. Tl;dr, I need math help and references for staying on-grid with strange rotations and shapes, but the ramble is a tale of woe specifically about why I got myself into this mess in the first place.
I've been messing around with a map idea I've had in my head for a while that I was considering calling ctf_Schism. I've spoken about it before, but I've had the idea ever since learning about the way ctf works under the hood. Essentially I was inspired by learning this: where the intelligence spawns, and the actual capture point, are entirely different things. But all official maps ignore this, and have them both in the same place. Naturally, I thought of conditions where separating them would make sense. I thought of a sort of "neutral zone" branching off from the middle/no-man's-land that the intelligence(s) would get delivered to (represented in my head as putting them in the backs of team-colored trucks which would drive off at the end of the round. The losing car would explode, purely for visual effect and my own amusement). With this in mind, I reasoned that the simplest way to make this would be a triangular central point, with the sides/spokes being the team bases and cap point. I have provided an incredibly shitty MS Paint diagram of the general idea:
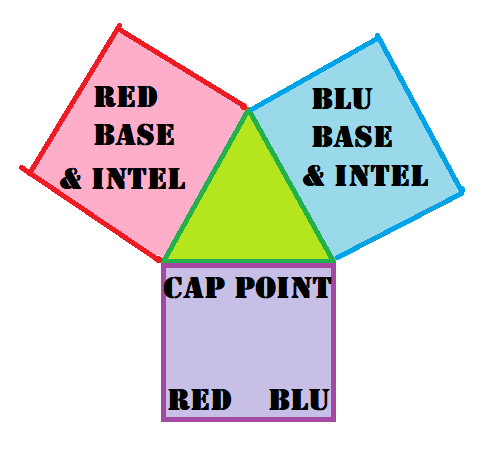
As you can see, that is not a rectangle. The Source engine is not happy about this in the slightest. I've already resigned myself to the fact that the midpoint is going to be Visleaf Hell regardless of what I do with it. All the gamemode logic is done and out of the way, that's not what I'm having trouble with, it's literally the shapes themselves that are the issue.
See, my initial hope was to make the central triangle equilateral, for balance (as everything should be). However- I discovered after some vertex fiddling, head-scratching, several rotations, headaches, and confused google searches... that I was doomed from the start. Apparently, the shape I was trying to create was mathematically impossible. You see, you're totally unable to create an equilateral triangle with points that align to a square grid, because of complicated math shit. So "Great, okay, fine," I think, "I'll just make it an isosceles triangle and set the odd length-ed side as the cap points" so it can at least have mirrored symmetry.
Once I figured that out, that's when I ran into another problem... I have no idea how to approach this. I have a general idea of what to do: make the Red and Blu bases instances so I can construct them on-grid while simultaneously having them rotated with skip brushes, figure that basic stuff out and then fine tune the layout from there. My problem is this: how do I do all this friggin math?? Has anyone else ever done stuff like this before and wrote it down so I could get an idea of what I need to do? Can the off-grid lines of an isosceles triangle have an on-grid length? And if so, how do I calculate that? Much like Soldier, I am a victim of the American education system, and can't do math shit beyond simple algebra to save my life. I had to google how to find the area of a triangle just to make the mid-point have a similar area to other ctf maps while not being a square. The diagonal lines of the isosceles triangle in my test vmf have a ratio of 2:1, and that's nice and all, but I have no idea if that's good or not, or how to use that information to help me.
And that's where I am now, folks. The most frustrating part about this to me, is that I've made the Red and Blu bases of this map at least twice already, and lost them to computer hardware failure. All I have left right now are people better than me who may have done geometry like this in Hammer before.
I've been messing around with a map idea I've had in my head for a while that I was considering calling ctf_Schism. I've spoken about it before, but I've had the idea ever since learning about the way ctf works under the hood. Essentially I was inspired by learning this: where the intelligence spawns, and the actual capture point, are entirely different things. But all official maps ignore this, and have them both in the same place. Naturally, I thought of conditions where separating them would make sense. I thought of a sort of "neutral zone" branching off from the middle/no-man's-land that the intelligence(s) would get delivered to (represented in my head as putting them in the backs of team-colored trucks which would drive off at the end of the round. The losing car would explode, purely for visual effect and my own amusement). With this in mind, I reasoned that the simplest way to make this would be a triangular central point, with the sides/spokes being the team bases and cap point. I have provided an incredibly shitty MS Paint diagram of the general idea:
As you can see, that is not a rectangle. The Source engine is not happy about this in the slightest. I've already resigned myself to the fact that the midpoint is going to be Visleaf Hell regardless of what I do with it. All the gamemode logic is done and out of the way, that's not what I'm having trouble with, it's literally the shapes themselves that are the issue.
See, my initial hope was to make the central triangle equilateral, for balance (as everything should be). However- I discovered after some vertex fiddling, head-scratching, several rotations, headaches, and confused google searches... that I was doomed from the start. Apparently, the shape I was trying to create was mathematically impossible. You see, you're totally unable to create an equilateral triangle with points that align to a square grid, because of complicated math shit. So "Great, okay, fine," I think, "I'll just make it an isosceles triangle and set the odd length-ed side as the cap points" so it can at least have mirrored symmetry.
Once I figured that out, that's when I ran into another problem... I have no idea how to approach this. I have a general idea of what to do: make the Red and Blu bases instances so I can construct them on-grid while simultaneously having them rotated with skip brushes, figure that basic stuff out and then fine tune the layout from there. My problem is this: how do I do all this friggin math?? Has anyone else ever done stuff like this before and wrote it down so I could get an idea of what I need to do? Can the off-grid lines of an isosceles triangle have an on-grid length? And if so, how do I calculate that? Much like Soldier, I am a victim of the American education system, and can't do math shit beyond simple algebra to save my life. I had to google how to find the area of a triangle just to make the mid-point have a similar area to other ctf maps while not being a square. The diagonal lines of the isosceles triangle in my test vmf have a ratio of 2:1, and that's nice and all, but I have no idea if that's good or not, or how to use that information to help me.
And that's where I am now, folks. The most frustrating part about this to me, is that I've made the Red and Blu bases of this map at least twice already, and lost them to computer hardware failure. All I have left right now are people better than me who may have done geometry like this in Hammer before.
Last edited:





